サイン波と矩形波 その1
さて、今回は「ガチで速くなる練習方法」の根底にある理論について書いてみます。
テーマはサイン波と矩形波です。
ちなみに サイン波と矩形波はどんなものか分かりますか?
まあ、理系じゃない人も居ると思うので簡単に説明しておきますね。
サイン波というのは簡単に書くと図1の様なものです。
図1 サイン波
サイン(sin)とは円運動をする物体の円周上の点の縦の位置です。
例えばsinθ といえば、角度がθの時の円周上の点の縦の位置です。 ちなみにコサインは横の位置です。
そしてサイン波とは簡単にいえば、横軸に角度を取り縦軸にこのサインの値を取って描いたグラフです。
円周上を動く点の位置の変化なので変化がとても滑らかになります。
次に矩形(クケイ)波です。 これは図2のようなものです。
図2 矩形波
矩形波はサイン波と違って連続的に変化しません。 文字通りに矩形、つまり四角い波です。
今回の話は車にかかる加速度(G)をサイン波の形にするべきか、或いは矩形波の形にするべきかというお話です。
最適解へのアプローチ(序論) に書いた通りに、車にかけることが出来る最大の加速度はタイヤの摩擦係数をμとすると、
μ[G]です。 つまりブレーキングの減速Gも横Gも加速Gも、或いはそれらを足しあわせたものも、全てμ[G]以内の加速度しか出すことができませんでしたね?
これがタイヤの摩擦係数だけで決まる物理的な限界値でした。
それでは車の性能を出すためには常に車にμ[G]の加速度がかかっていれば、それ以上ない最高の性能を出している事になりますね。 そしてその性能の出し方には、大きく分けて二通りのアプローチがあるわけです。
それが今回のサイン波と矩形波の、どちらの形で出すべきか、という話になります。
まず始めにサイン波の話をしてみましょう。
ぜんぜん難しく考えなくても大丈夫です。 これは色々な所で言われている摩擦円の話そのものですから。
摩擦円の話はいいですね?摩擦円を意識した運転については雑誌など色々な所に書かれているのでこのHPでは省略していましたが、ここでちょっとおさらいをしてみましょう。
まず始めにこちらを読んでおいて下さいね。
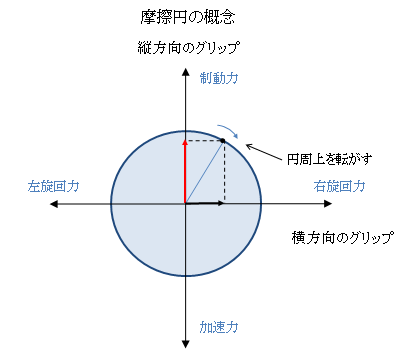
図3 摩擦円のイメージ
さて、それではここで摩擦円を考慮してブレーキングからコーナリングをしてコーナーを抜ける所までの運転を考えてみましょう。
摩擦円の理論によると、最大の力でブレーキングをしている時にはタイヤの横方向の力はないことになります。
最大の力とはもちろん今回のμ[G]の減速Gを出している時です。 μをタイヤと路面の平均的な摩擦係数とすると、これは
0.9[G]となりますね。
このままではタイヤには横方向の力がないため曲がれません。 実際にロックすれすれのブレーキングをしながらハンドルを切っても車は真っ直ぐに行ってしまい曲がりませんね?
そこで車を曲げるためにはタイヤの横方向の力を発生させる必要があります。 そのためにはハンドルを切ると同時にブレーキを少しずつ緩めて行き、図3のように、あたかも摩擦円の円周上を転がすようにブレーキを少しずつ抜きながらハンドルを切っていきます。
ブレーキを緩めると縦方向の減速Gが減るため、横方向に加速度を生み出すことができます。
もっと簡単言うと、ブレーキを緩めることで縦のグリップが減る代わりに横のグリップが出てくるわけですね。
この横グリップが曲がる力になるわけです。
摩擦円の理論によると、ブレーキを緩めれば緩めるほど横方向のグリップを多く使うことができるようになります。
そして一般に言われているのは、この理論よりブレーキを最も緩めた時に一番大きい横グリップを発生できるため、最も大きな舵角でハンドルを切っている(切れる)ことになるというものです。
つまり減速Gが存在しない時にマックスの舵角になって最大の横Gを発生する、と言うことですね。
この、車にかかるGを摩擦円の円周上で転がすというイメージを可視化する例として、漫画などでコップに水を入れてコップの縁に沿って水を転がす、と言った例を聞いたことがある人も居ると思います。
コップの水の話はつまり、この摩擦円の話を言っていただけだったんですね。
さて、一般に言われている摩擦円の話は、大体こんな説明が主流だと思います。
ただ摩擦円の話では円周上をどのように動かすか、という話はいつもごっそり抜けていますね。
例えばゆっくり動かすのか、あるいは速く動かすのか。 定速で動かすのか、加速度的に動かすのか。
それを考えるために今回は、摩擦円の図を時間と加速度の関係を表すグラフに展開してみましょう。
おさらいした上記の、一般的に言われている摩擦円の上を転がすセオリー通りの運転は図4の様になるでしょう。
これが正にサイン波です。
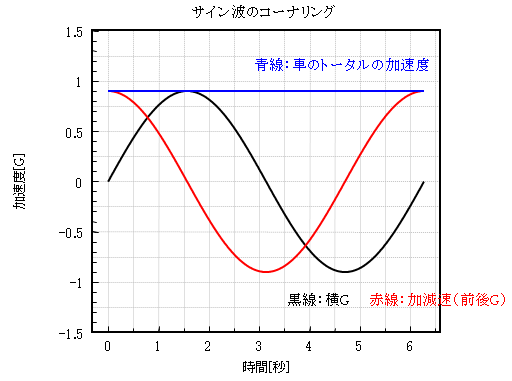
図4 サイン波コーナリングのイメージ
赤い線が加減速のGで、黒い線が横Gです。 赤い線は0よりも上の方向が減速Gで、下の方向が加速Gを表します。
それでは時系列で見てみましょう。 まず始めに0秒の時に赤い線が最大の0.9[G]を出していますね。
これは当然ブレーキがロックすれすれでマックスの制動力を出している時です。
その時には当然横Gの黒い線は0[G]です。 そして赤い線が下がると共に黒い線が上がっていっていますね?
ちなみに赤い線と黒い線を足したもの、つまり横Gと加減速Gとを足したものが青い線です(これはベクトルの足し算です)。
タイヤの最大のグリップを使って摩擦円の円周上を動いているので、当然合計の青い線は常に0.9[G]となります。
つまりこのグラフでは常にタイヤが最大の力を発揮していることになりますね。
次に横Gの黒い線が上がると同時に赤い線が落ちていき、黒い線が最大の時には赤い線はちゃんと0になっていますね?
つまり、横Gが最大になる時には加減速は無いことになります。(ちなみに、実際にデータロガーを見ると確かにそうなっています)
そして1.5秒辺りを過ぎると今度は赤い線が0よりも小さくなっていきます。 これは今度は車が加速しているという意味です。
実際の走行では、 ここではクリップを過ぎてアクセルを踏んでいるイメージですかね。
そして車の加速度が上がると共にまた黒い線が落ちていっていますね?
これも摩擦円の理論によって、今度は加速のためにタイヤの縦のグリップが使われるので、また横グリップが減って小さな横Gしか出せなくなることを表しています。
そして赤い線が最大の加速Gを出している時にはちゃんと黒い線は0になっていますね。
つまりここでは直線を0.9[G]の加速度で加速している状態です。
サイン波の定義自体が円周上を動く点の縦成分なので、摩擦円を展開するとサイン波になるのは当たり前ですね。
ちなみに図4では図3の摩擦円でいう12時の位置の角度を0としているので、sinが横G、cosが加減速Gとなっています。
つまり図4は摩擦円の円周上を12時の位置から3時の位置に向かって定速で動く点の、横の成分と縦の成分、つまりsinとcosをそれぞれ黒と赤でプロットしただけです。
高校時代に習った三角関数は、こんな所で生きたりするんですね(笑)。
(ちなみに黒い線(横G)がサイン波ならば、赤い線(加減速G)はコサイン波ですが、これは位相がπ/2ずれているサイン波と同意です。 cos θ = sin ( π/2 - θ ) より )
とまあサイン波コーナリングの説明はこんな感じです。 この走り方をしてデータロガーで測定した加速度のグラフを見ると、実際にこの様になっています。
さて、この走り方は車の性能を最大限に出しているように見えますかね。
説明がエレガントなこともあってこの走り方は一般に良いと言われていて、色々な所に書かれているものです。
よってこれを目指してみるのも一つの手でしょう。
どこかに詳しく書くかもしれませんが、「ブレーキを残すコーナリング」というのは正にこれの事を言っているだけです。
今回の例を具体的な操作にすると、クリップまでどんどんブレーキを緩めて行くと同時にハンドルを切り足して行き、クリップでブレーキを離すと同時にハンドルの舵角が最大となり、クリップを過ぎると同時に加速を始めてハンドルを戻していく、といったブレーキを残す走り方に適合するでしょう。
別にこの走り方が間違っているわけではありませんし、これは結構多くのプロが指導する運転方法でしょう。 そして素人は殆どの人がこの運転が出来ていないでしょう。
だからまず始めにこの運転をマスターするのも良いと思います。
さて、しかしながらこの運転が最も速い運転、つまり「最適解」かというと、私は違う見解を持っています。
そもそもこの運転ではコーナリング中に舵角が一定になる瞬間は全く無いことになりますね。
つまりセオリー通りのサイン波コーナリングをするとなると、ここで勧めている舵角一定の運転は間違っていることになります。
また、最大の遠心力に対向する操作に書いた最大の遠心力に対向するアクセル操作、一般に言われている言葉で言うなら、「バランススロットル」も無いことになります。
ちなみにこれは私の個人的な意見ですが、このサイン波の運転を勧めている人の多くは後輪駆動車に特化した話をしている気がします。 特にカート出身のフォーミュラカーをメインにしたドライバーに、このブレーキを残す説明をする人が多いような気がします。(ここでは省略しますが、カートではこの運転が基本ですから)
特にFF車に乗っている人ならば経験があると思いますが、クリップから加速とともにすぐにハンドルを戻すことはあまりないと思います。 もしあったとしたら、元々スリップアングルが一番曲がる所を通り過ぎていたのを適正値に戻したか、或いはスピン挙動などになって明らかに失敗したケースでしょう。
通常は前輪に駆動力がかかっている時にハンドルを戻すとアンダーステアに行くと思います。
こちらに詳しく書かれていますが、FF車では加速すると操舵輪の縦グリップが喰われてしまうので、ただでさえ曲がりにくくなるはずですから、そこでハンドルを戻して更にCPを減らす事は普通はしないと思います。
FF車では多くの場合、コーナーの終わり付近に来て初めてハンドルを戻すケースが多いでしょう。
さて、そこで次に矩形波コーナリングの話に行きましょう。
まずは同じ様に時間と加速度のグラフを見てみましょう。
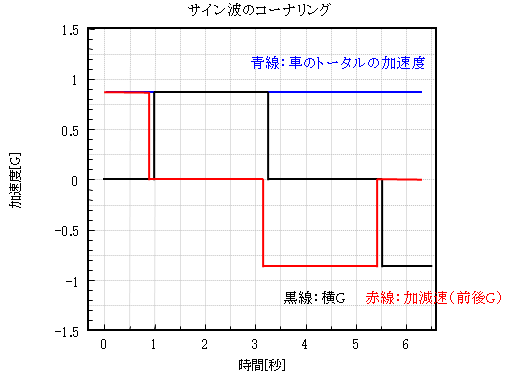
図5 矩形波コーナリングのイメージ
同じく赤が加減速G、黒が横Gです。 今度は滑らかさが全く無くなっていますね。
サイン波コーナリングではブレーキをゆっくりと緩めて減速Gが減ると共に、横Gが増えて行きました。 でも今回はブレーキは一切残していません。 横Gも徐々にではなく一気に発生しています。
摩擦円で言うならば、ゆっくりと円周上を転がるのではなく、12時の位置から瞬時に3時の位置に移るイメージですかね。
私はこの運転の方がサイン波運転よりも速い、最適解に近い運転だと考えています。
どうしてでしょうか?? 少し考えてみて下さいね。 今までの項にヒントは書かれています。
続く…
Back Top