コーナリングの最適解 その2
さて、前回の続きです。
それでは式が出来た所で、早速具体的な数値を入れて計算してみましょう。
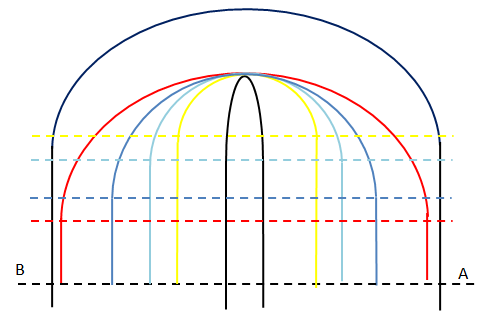
図1
Rの異なるコーナーのライン。
今回もタイヤの摩擦係数μ は、タイヤと路面の平均的な摩擦係数0.9とし、今回は車重は関係ありませんが一応1200[Kg]としておきましょうか。
そして図1のA点の進入速度を100[Km/h]として、A点の位置をクリップから100[m]の位置としましょう。
つまり、旋回半径Rは100[m]まで取れる、ということですね。
ブレーキングの制動Gは摩擦係数が0.9なので、最適解へのアプローチ(序論)より4つのタイヤの限界である0.9[G]としましょう。
そして旋回が終わってから、B点までの直線区間の加速度は、まず始めに0.5[G](=9.8×0.5[m/s2])としておきましょう。
重力加速度g は、当然9.8[m/s2]ですね。
この条件で、Rを1[m]から100[m]まで計算してみましょう。
さてさて、それではどうなるでしょうか。
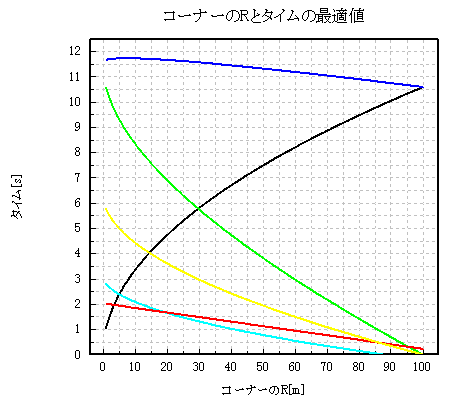
グラフ1 コーナーのRと区間タイムの最適値
それではグラフの説明です。
横軸はRの大きさ、縦軸は時間です。
黒い線は、旋回中の時間です。水色の線は、ブレーキを踏んでいる制動時間です。赤い線は、侵入位置A点を過ぎてからブレーキを踏むまでの時間です。そして黄色い線は、旋回が終わってから、B点までの直線区間の加速時間です。
緑色の線は、直線区間全てを足した時間です。
そして、一番上の青い線が旋回区間と直線区間を足した、A点からB点までのトータルの区間タイムです。
さて、このグラフをどう見ますか??
まずRが大きくなるほど旋回時間は長くなり、直線区間を走る時間は短くなっていますね。
これは感覚的なものと一致しているかな??
ただ旋回している時間は、Rが大きくなると着実に増えていますね。
これはつまり、旋回速度が上がっても、距離が長くなることによる距離損の方が上回る、ということでしょう。
その代わりに直線区間を走る時間は、Rが大きくなるほど当然短くなっていますね。
そして、青い線を見れば、旋回中の時間(黒線)の上がり具合よりも直線区間を走る時間(緑線)の下がり具合の方が大きく、結果的にRを大きくすればする程タイムが速くなっている事が分かりますね。
その他にもこのグラフからは、色々なことが分かります。
例えばRが5[m]までは、旋回時間よりもブレーキを踏んでいる、止める時間の方が長いということ、30R程で旋回時間と直線の時間が入れ替わること、などなど。。。
まあ、あまり詳しく書くのはやめておきますが、これを見ればバトルの追い抜きラインなども見えてくるでしょう。
ぜひぜひ、色々考察してみて下さいね。
ちなみに、水色の線が87R辺りで0より小さくなっていますが、これはどういう事か分かりますよね?
これは「ブレーキを踏まなくても限界を超えない旋回速度で曲がれる」という事です。
簡単に言えば、これ以上のRならば、100[Km/h]の速度からノーブレーキで曲がれるという意味です。
つまり100[Km/h]の速度で進入すると、87R以上では旋回中にタイヤのグリップを余らせることになります。
よって今回のグラフでは、87[m]以上は無視して下さい。
(グラフではブレーキを踏んでいる時間がマイナスとなり、旋回速度が進入速度よりも高くなってしまいます。)
さて、このグラフよりRが7[m]辺りで区間タイムは極大値を迎えて一番遅くなり、それ以降はRが大きくなるほど区間タイムが速くなる事が読み取れますね。
そこでこのグラフより、次のようなことが言えそうです。
区間タイムは、旋回中に最大限の横G(今回の例なら、タイヤの摩擦係数は0.9なので0.9[G])を維持できる、最大の大きなRを描くラインが一番速い、と。
でもこんな疑問を持つ人も居るかな?
最大の横Gより少し小さくても、大きく曲がった方が速い領域があるのではないか?、と。
うむ。
それでは横Gが、0.9[G]ではなく0.8[G]だったらどなるか計算してみましょう。
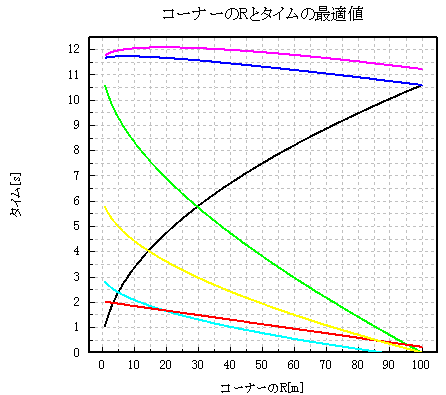
グラフ2 コーナーのRと区間タイムの最適値 (ピンクの線が横Gが0.8[G]の時の区間タイム)
グラフ2は、先ほどのグラフに0.8[G]の時の区間タイムのピンクの線を加えたものです。
0.1[G]落ちただけで、かなり遅くなりましたねぇ。
これは旋回時間が増えただけではなく、速度を落とさないといけないため、直線区間も加減速に時間が掛かるのも理由でしょう。
ただ調べてみるとほとんどが、旋回時間の増加だということも付け加えておきます。
今度は極大値のRが20[m]に移動しているのも興味深いですね。(つまり、20Rのラインが一番遅い事になりますね。)
ちなみに横Gが小さくなればなるほど(旋回速度が遅いほど)、極大値は右に移動します。
これは、コーナリング速度が限界の大分手前であれば、小さく曲がった方が速いことも大いにあり得る、ということですね。
(これについては、ちょっと考えてみて下さい)
さて、このグラフより最大の横Gよりも0.1[G]小さい場合、つまりタイヤのグリップが少し(0.1[G]分)余っている場合には、最大の横Gである0.9[G]を出している車が40Rほどのラインで曲がっているタイムに、85Rほどのラインで初めて並べることになります。
つまり、タイヤのグリップを余らせて大きなRを描くラインの区間タイムは、余程ラインのRの差(今回の例だと倍以上)がない限り遅いと言えるでしょう。
つまり今回のモデルではやはり、
「区間タイムは、旋回中に最大限の横Gを維持できる中で、最大の大きなRを描くラインが一番速い」、と言えそうですかね。
ところで今回計算した車は、加速Gを0.5[G]としましたね。
これはかなり大きめの加速力を持っている車だと思います。
最適解へのアプローチ(序論)に書いたように、加速Gはタイヤの摩擦係数をμ とすると、μ[G]以上の加速は不可能です。
これは当然全てのタイヤが最適値を出す時なので、4輪駆動車以外には不可能です。
もしも2輪駆動車で、前輪と後輪の荷重が同じだとしたら、0.9/2=0.45[G]が出せる加速度の最大値となりますね。
まあ実際には後輪駆動車は加速時に後輪の荷重が増えるので0.45[G]以上出せるでしょうし(後ろにエンジンがある車なら尚更)、逆に前輪駆動車は加速時に荷重が減るため、難しいでしょう。
またタイヤの限界以前に、100[Km/h]前後の速度から0.5[G]出そうとすると、エンジンのパワーもかなり必要となります。
ちなみに今回の1200[Kg]の車重だと、およそ222馬力が必要となります。
この様にこの例では、エンジンのパワーもタイヤのトラクションも大きめですが、これよりも小さい加速Gしか出せない車では、極大値は存在せずに区間タイムはRが大きくなるほど一直線に速くなることを書いておきます。
ちなみに加速Gが0.3[G](134馬力程度)だと以下のようになります。
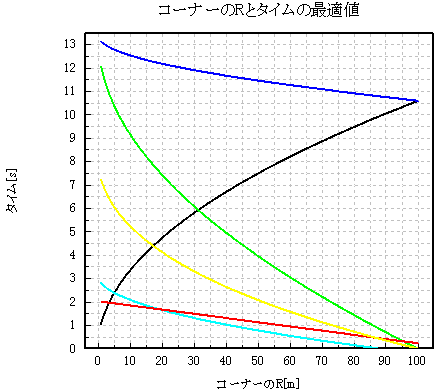
グラフ3 コーナーのRと区間タイムの最適値 (加速Gが0.3[G]の時)
では次に、ハイパワーで強力なトラクションを持つ四輪駆動車だったらどうなるのかを計算してみましょう。
今回は四駆で、4つのタイヤのグリップで出す事が可能な加速度の最大値である0.9[G]を出すと仮定して計算してみましょう。
他の条件は全く同じです。
現実に0.9[G]の加速Gを出すのはかなり難しいと思いますが、極端な例の方が分かりやすいと思います。
それでは計算してみましょう。
区間タイムを見てみると以下の様になります。
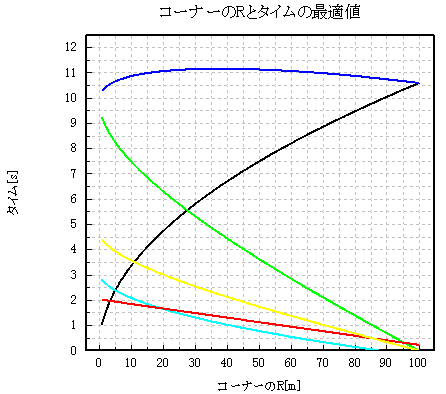
グラフ4 コーナーのRと区間タイムの最適値 (加速Gが0.9[G]の時)
減速(ブレーキング)は今までのモデルも4つのタイヤの限界まで使っていたので、立ち上がり加速(黄色の線)が速くなった分だけ当然区間タイムは速くなっていますね。
そして注目するべき所が、区間タイムの極大値が大きく動いていることです。
大体38R位ですかね(正確には37.73Rから38.03Rまでの間は同じ)。
つまりこの車のケースでは、38R近辺が一番区間タイムが遅いことになります。
よって今回は、耐えうる最大の旋回速度を出していても、大きいRの方が区間タイムが速いとはならないようです。
グラフ4より38Rよりも大きいか、或いは小さい方がタイムが速いことになりますね。
このグラフは1Rから計算していますが、まあ実際に半径1[m]で曲がれるかどうかは置いておいて、Rが一番小さい時が一番区間タイムが速いようです。
そしてRが大きくなるにつれて区間タイムが遅くなっていき、38Rを超えるとまた区間タイムは速くなっていきます。
先述の通り100[Km/h]の侵入速度だと87Rよりも上は存在しないため、87Rの区間タイムを見てみると10.78秒です。
これがRを限界まで大きくした時のタイムです。
そしてRが1[m]の時には10.29秒です。 よってこのケースでは、小さいRで曲がった方が区間タイムは速いことになります。
ちなみに一番遅い37Rでは、11.11秒となります。 つまり最も速いラインと比べて0.8秒程度も遅いことになります。
よって、37R近辺のラインを選ぶと区間タイムは遅くなるため、このラインは避けるべきでしょう。
今回の計算より、「車の加速力によってレコードラインは異なる」と言えるでしょう。
ある加速度を境に、Rを小さくした方が速くなることがあるわけです。
区間タイムに限って言えば、そのある加速度とは、0.9/2=0.45[G]
辺りです。
ただこれを数学的に証明するのはちょっと面倒だったので今回は数値計算でこういう結論としましたが、区間タイムを全て足したもの(青いライン)を(傾きが知りたいのだから)rで微分してやって、その値がある加速度(恐らく、μ /2[G] )以上になるとプラスの値を取らない、ということを証明してやれば良いでしょう。
微分が得意な方、
ぜひ誰かやって教えて下さい(笑)。
さて、今回の計算で分かったことは、「加速力が0.45[G]以内程度の普通の車であれば、区間タイムは旋回中に最大限の横Gを維持できる中で、最も大きなRを描くラインが一番速くなる」
が、「加速力が0.45[G]以上のハイパワー&高トラクション車では、出来る限り小さなRを選んだ方が区間タイムが速いことがある」といった感じでしょう。
これはスローイン・ファストアウトは速いのかに書いた、ハイパワーの四駆の車は立ち上がり重視のV字ラインが速いと言われている、一つの根拠になりそうですかね??
今回の結果を参考にして、後は実際に走るコースで取れるラインの選択幅を考慮して、加速力を含めて今回私がやったように先述の式に自分の車の数値を入れて計算すれば、最も速い区間タイムが出るラインが決まるでしょう。
(私は計算に自作のソフトを使いましたが、Excelなどでも出来るはずです)
これが今回のモデルによる、その区間のラインの「最適解」です。
さて、それでは今回の「区間タイムが一番速いライン」を常に選べば、コースを最も速く走れるのでしょうか??
当然違いますね?
そのために布石として、距離損とスピード損 とスローイン・ファストアウトは速いのかの話を書いておいたわけです。
区間タイムが同じでも、その前後の速度が異なれば当然コースのタイムは変わってきましたね?
今回はA点の進入速度はどのラインでも同じですが、B点の脱出速度によっては、例え区間タイムが遅くても後で逆転する可能性がありますね?
そんな訳で、今回は「区間タイムの最適解」であって、「コースの最適解」と言うにはちょっと足りません。
そこで次に、B点の脱出速度もラインごとに調べてみましょう。
続く…。